Depuis que je pratique l’informatique, c’est à dire, 1981 je me suis toujours passionné pour les courbes fractales.
Pour ceux qui ne connaissent pas, et les autres d’ailleurs, je vais tenter de vous expliquer simplement le principe de base par l’exemple. Je ferai abstraction des calculs mathématiques nécessaires à la réalisation de telles images.
Qu’est-ce qu’une fractale ?
Une courbe fractale est un dessin composé de segments dont la forme de base va être reproduite à l’infini sur chaque segment. Mouai !, je vois déjà un gros point d’interrogation sur vos têtes.
Nous allons prendre pour exemple la courbe de Von Koch en partant d’une ligne droite, rien de bien compliqué jusque là.
La courbe de Von Koch
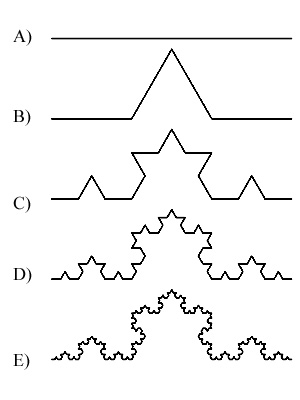
A) On part d’une ligne droite
B) Sur cette ligne droite on dessine un triangle équilatéral sans la base. Cela nous donne ce que j’appellerai « La forme de base »
C) Maintenant, nous allons appliquer cette « Forme de base » à chaque segment de droite, les horizontaux mais aussi ceux du triangle.
D) On répète la même opération sur chaque segment de droite, vous commencez à comprendre ?
E) Même motif même punition et ainsi de suite….. jusqu’à l’infini si on a envie.
Chaque étape s’appelle une itération, ici nous en avons effectué quatre, de B à E et on peut en faire autant que l’on désire. On utilise à chaque étape la même méthode qui se reboucle sur elle même, c’est la récursivité.
Petit inconvénient, l’oeil n’arrive plus à distinguer chaque partie de la courbe.
Pour pouvoir visualiser une zone précise, il va falloir grossir une partie du tracé pour en distinguer les détails. On parle alors d’explorer une région; alors, explorons…
Les courbes ou les flocons de Von Koch offrent une exploration très limité, nous allons passer à la vitesse supérieure
La fractale de Mandelbrot
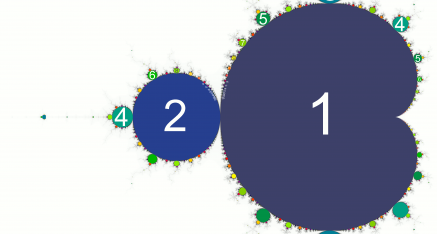
La fractale de Mandelbrot est beaucoup plus complexe et offre des possibilités d’explorations bien plus intéressantes. En ajoutant des variations de couleurs on a vraiment l’impression de naviguer dans un autre monde.
La base est constituée d’un cardoïde autour duquel se disposent des bourgeons en forme de cercles.
Voyons cela de plus près et cliquez sur l’image ci-dessous.
Maintenant, regardons une exploration de régions. Les logiciels de création de fractales permettent d’aller dans toutes les directions, c’est à vous de décider du voyage.
L’ensemble de Julia
Du même acabit, il existe l’ensemble de Julia constitué de deux parties complémentaires… Cliquez ci-dessous.
Les fractales de Lyapunov
Non moins intéressantes, les fractales de Lyapunov offrent une autre vision tout aussi mystérieuse de l’image mathématique. Cela m’a toujours fait penser à un liquide sur une plaque de verre qui l’on aurait étalé.
A chacun d’imaginer ce qu’il voit dans les nuages…
Voyage au coeur d’une fractale de Lyapunov
Voyage au sein d’une fractale en 3D
La puissance de calcul de nos machines actuelles permettent de calculer et de réaliser des fractales en trois dimensions. On est bien loin de notre courbe de base de la fractale de Von Koch…
Les fractales dans la nature
L’être humain a-t-il vraiment créé les fractales ? D’un point de vu mathématique et logiciel, oui certainement, mais la nature ne nous a pas attendu pour faire cela. En regardant à la loupe la structure d’un arbre nous y retrouvons le principe de la fractale de Von Koch ou encore d’une simple fougère à trois itérations.
Le plus criant est à mon avis le choux Romanesco, j’en suis resté sur mon postérieur la première fois que j’en ai vu un. Le principe est respecté à la lettre, une forme de base répétée à presque l’infini.
Si vous avez encore un doute, cliquez sur les images ci-dessous et zoomez dessus, CQFD.
Ici se termine cet exposé, si vous voulez continuer l’exploration du monde fractal, je vous conseille le logiciel « UltraFractal » qui permet de créer de petites merveilles.
Pour ceux qui veulent aller plus loin, de nombreux articles existent sur la toile, il n’y a que l’embarras du choix.
Bon voyage dans cet aspect du monde numérique qui se mêle étroitement avec celui du réel.
Daniel Delevoye
ShareMAI
2013